合规的股票融资工具

倪世杨 Z0019629

每个金工学生都在学校学过BSM。这一划时代的公式不仅让期权产业蓬勃发展，更是打开了Q-quant世界的大门，让无数理工科学子加入到金融行业。但金融毕竟不是工科、不是数学，鲜有种瓜得瓜种豆得豆的确定性；交易也不是清爽靓丽的模型推导，没哪个变量不包含现实的噪音。实战里重要的是“有用”，而“正确”仅在影响“有用”的范围内有意义。带着这样的目光，我们重新推一遍BSM，看看哪些假设是可以接受的“模糊的正确”，哪些是需要被调整的“精确的错误”。

本文分上中下两篇。上篇讨论几何布朗运动的优势与局限，并阐述其三种形式对应的直觉理解。 中篇详述Black-Scholes Equation推导过程，探讨做空限制、交易摩擦如何影响该模型推导。下篇从BSM Equations推导至BSM Formula，用通俗的语言解释Risk-neutral的含义。本文力求将数学语言落实到直觉上，让未接触过金工知识但有一定统计基础的同行们也能看懂BSM的推导，从而参与到对模型逻辑的思考当中来。

GBM的优势与局限

Geometric Brownian Motion(几何布朗运动)是描述股价变动最简单的模型。它说了这样一个故事：持有一支股票，下一秒的资本利得既有确定性，也有随机性。用符号写出来，这个模型就看起来fancy许多：

    

    

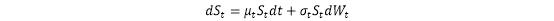
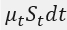
部分是股票价格的确定性变动。比如我们认为中海油股票价格每年固定能涨10%，现在中海油价格是100元/股，那持有1秒的确定性收益就是

    

    

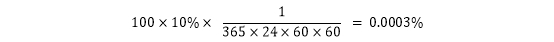
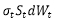
是随机部分，个服从正态分布的随机变量，均值为0，标准差为

    

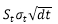
。假如中海油的年化波动率为20%，那1秒内随机部分的标准差为

    

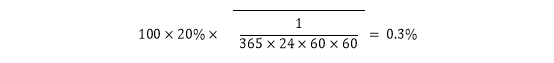
也就是说有95%的概率随机部分绝对值小于0.6%。

股价变动真能拆成确定性+随机性部分么？往深了说这是个认识论问题，可能也永远没有人能知道答案。股价变动可以被看做确定性+随机性之和吗？这个模型似乎足够灵活，经过微调后能解释很多现象。比如

-         标准化收益的正态分布特征：日度的资本利得除以日度波动率，所得分布基本是正态的

-         随着时间窗口变窄，波动比趋势要衰减得慢得多：观察窗口越短，随机波动幅度的衰减速度远不如确定性收益，这和我们提倡“不要频繁做短线”的直觉相符

-         收益肥尾分布的特征可以通过在

    

上施加自相关性得到。

既然这个模型能解释些事情，形式上又简单，那不妨先用着。这恐怕才是用GBM来模拟资产价格的真实理由。

GBM也有它的局限。最重要有以下两点

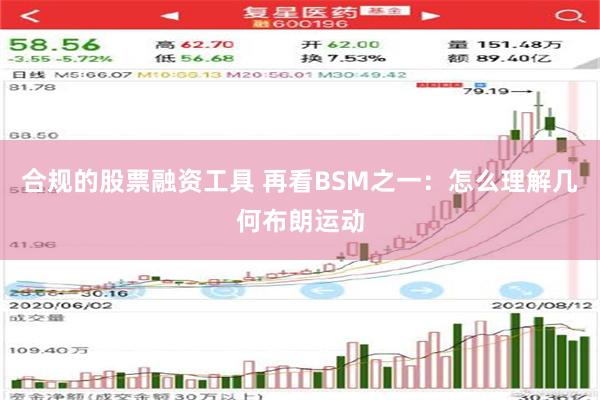
1. 最重要的是它无法模拟跳空，因此用GBM来模拟资产价格会严重低估跳空风险。

上图为WTI的日线走势图。4月12日触及阶段性高点87.67美元，随后持续回落，截至今日累计跌幅近10%。期间出现过两次反弹，分别出现在4月26日和5月20日，形成两个高点R2 R1。上周刚刚创出阶段性新低，预计空头趋势大概率将会延续。伊朗爆出增产消息，将对多头信心形成冲击，本周国际油价有可能加速下跌。

2. 它忽略了流动性风险。几乎所有模型都假设了世上存在一种东西叫“实时价格”。事实上投资者能拿到的只有当下的盘口，而盘口都有点差。因此包括GBM在内的几乎所有模型都忽略了流动性风险，这在交易十分频繁时会低估滑点，在波动极端时会低估市场风险。

GBM的三种形式

GBM有三种形式：

    

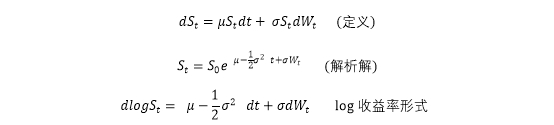
定义由直觉而来，为的是表达“短期资本利得由确定性和随机性部分组成”这一观点。

定义到解析解靠猜。这一步属于解偏微分方程，本质上就是靠猜出来的。

解析解到log收益率形式靠求导，这里要用到伊藤引理。dlogst实际上是在问，时间t往前走一小段dt，logst会变化多少。这相当于要求出

    

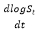
，再乘上dt即可。注意到logst是st的函数，而st又是t的函数，用心的读者可能很容易想到高中学过的“复合函数求导”。事实确实如此，只是由于st与t的函数关系里包含着随机性，“复合函数求导”的公式得变一变，这就是伊藤引理。

我认为log收益率形式是理解GBM最直觉的形式。这个形式的含义是“股票在短期内的log收益率服从正态分布”。短期内的log收益率可以近似理解为“收益率”，所以这个形式是在说“股票短期的收益率服从正态分布”。这就很有模型从简的味道了。“正态分布”的假设并没有听上去限制性那么强，因为波动率本身可以有时序结构，甚至也可以是随机过程，这样股票短期的收益率只是条件正态分布，其非条件分布则会非常灵活，足够承载实战里的复杂性。

Log收益率该怎么理解

由log收益率形式可以轻易得到解析解，把dlogst累加就行。Log收益的妙处便在于其严格可加性。平时我们谈涨幅，算的都是简单收益率。比如中海油从100涨到130，简单收益率便是30%。简单收益率的问题是并非严格可加的。从100涨到130是30%，从130涨到150是15%，可是从100到150是50%，并非30%+15%=45%。

那有没有办法定义一种收益率是严格可加的呢？log收益率就是。从100涨到130的log收益率是log(130/100)，从130到150是log(150/130)，而从100到150是log(150/100) = log(130/100) + log(150/130)，严格可加。

Log收益率的缺点是不够直观：虽然它可以被解释呈“连续计息对应的年化收益率”，但现实里没什么东西是真正“连续计息”的 。我认为log收益率更好的理解方式是它就是另一版本的“收益率”。说到底收益率是个人为定义的概念，收益本身才是客观存在的。既然如此，那我就能定义各种算法的“收益率”，只要计算结果能被成功还原成收益即可。